Stochastic Gradient Descent는 Batch Gradient Descent에 비해 최적값에 수렴할 가능성이 적으나, 적은 데이터를 사용하여 손실을 계산하고 모델을 업데이트 하므로 계산 속도가 빠르며 여러 번 반복할 경우 일반적인 batch 결과와 유사하게 수렴 가능하고 Batch Gradient Descent에서 빠질 지역 최소값에 빠지지 않고 더 좋은 방향으로 수렴할 가능성도 있음
※ Batch Gradient Descent가 최소값에 수렴함을 보장한다고 하였으나 그 값이 지역 최솟값일지 전역 최솟값일지 모름
일반적으로 Neural Network를 학습시킬 때는 SGD를 사용함
단순히 SGD 방식만 사용할 경우 노이즈가 많고 안장점에서 방향을 잘 못잡거나 학습 속도에 문제가 있는 경우가 많음
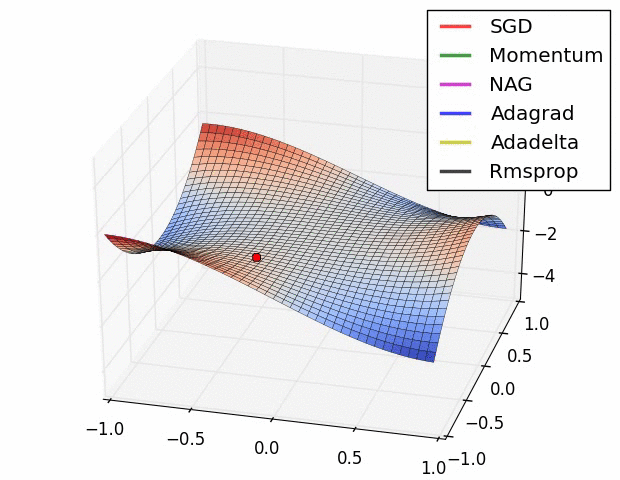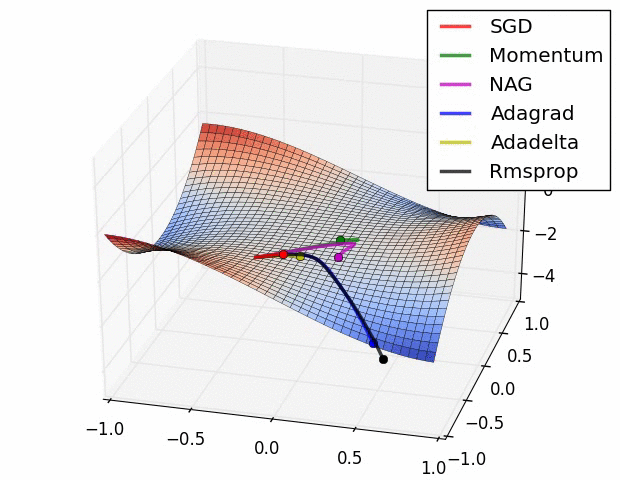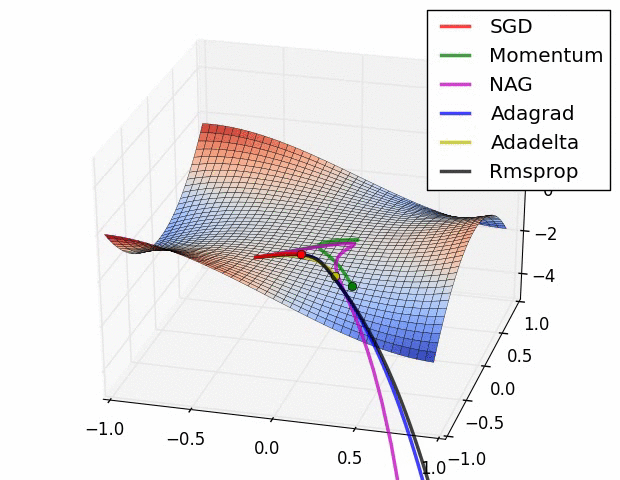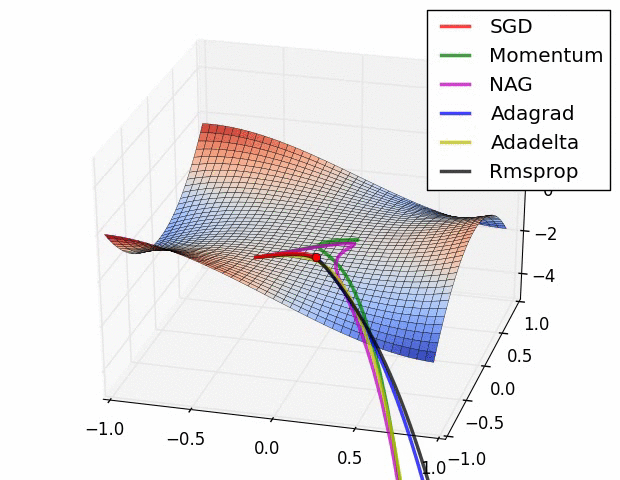
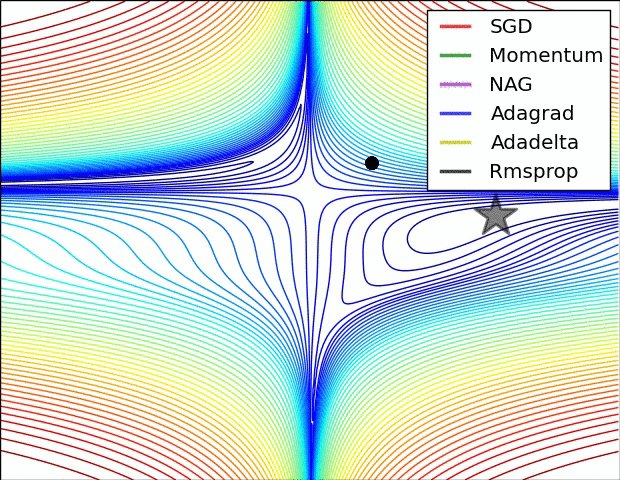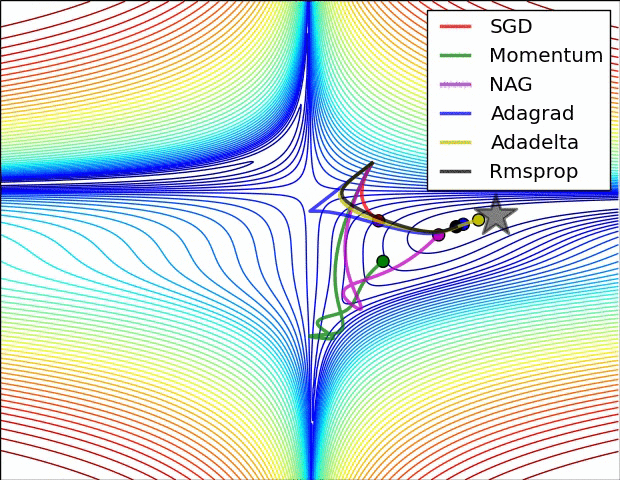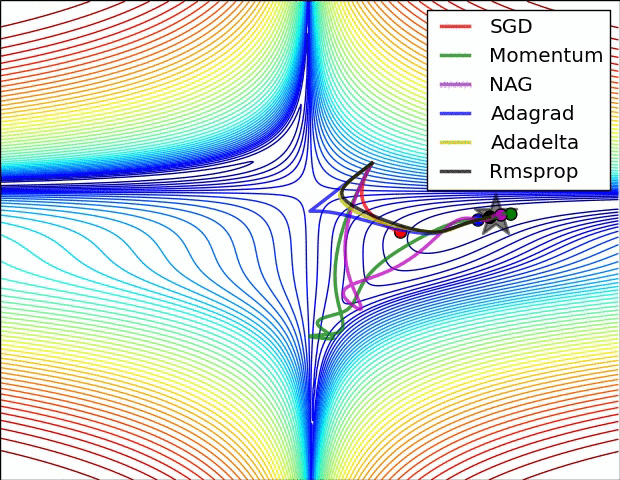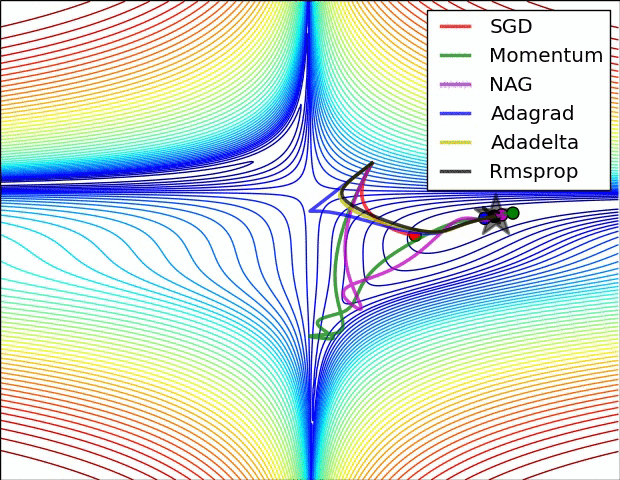
이를 해결하기 위해 SGD의 변형 알고리즘들이 있음
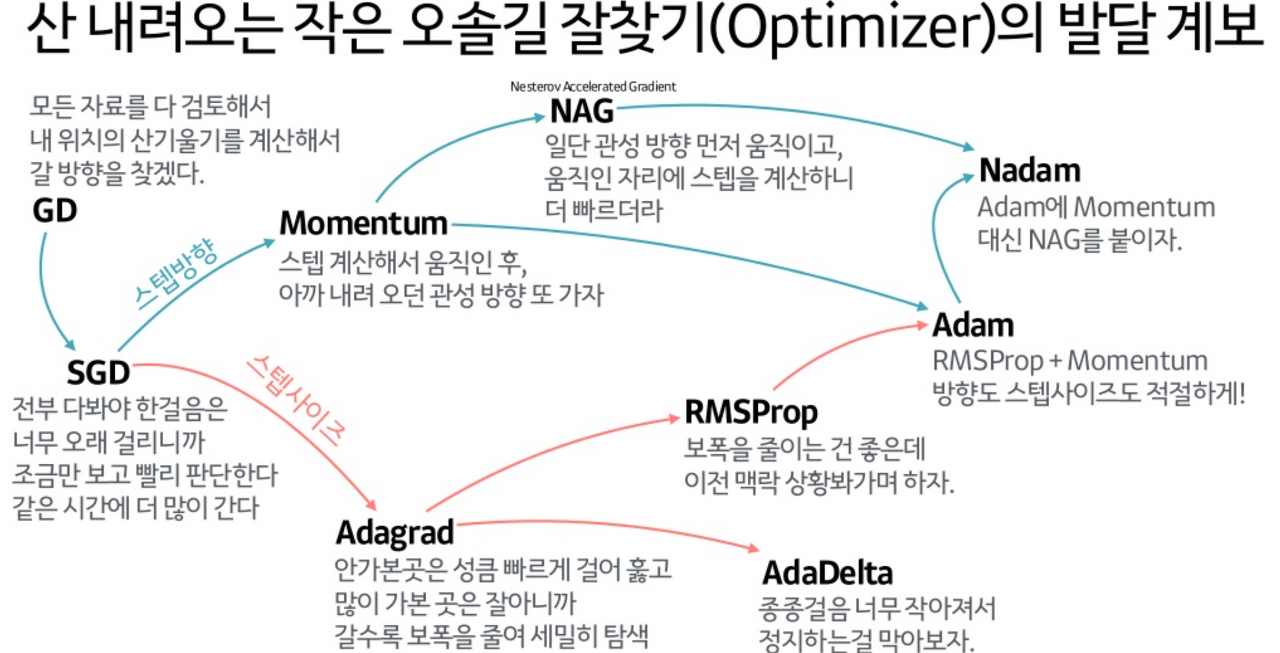
Momentum
Gradient Descent를 통해 모델이 업데이트 되는 과정에서 일종의 관성을 주는 방법
모델 업데이트 시 현재의 gradient를 통해 이동하는 방향과 별개로 과거에 이동했던 방향을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동하는 방식
해당 정도를 결정하는 momentum을 얼마나 줄 것인지 설정 필요
장점
- momentum에 의해 지역 최솟값을 빠져나올 경우를 기대할 수 있음

- 기본 SGD 방식에 비해서 momentum을 통한 자주 이동하는 방향에 대한 관성에 의해 더 빠르게 수렴 가능
단점
- 기본 SGD 방식에서는 단일 데이터에 대해 손실 계산, 모델 업데이트 하였으나 과거 이동 방향에 대한 momentum에 의해 추가적인 변수가 필요하고 그에 따라 필요 메모리도 증가하게 됨
Nesterov Accelerated Gradient (NAG)
Momentum 방식을 기초로 하나, Gradient 계산 방식이 다름

Momentum 방식에서는 현재 위치에서의 gradient와 momentum을 독립적으로 계산하고 합쳤지만 NAG는 momentum에 의한 이동을 먼저 가정하고 그 자리에서의 gradient를 구하여 업데이트함
장점
- momentum 방식에 비해 효과적으로 이동할 수 있음
- momentum 방식은 멈춰야 할 시점(전역 최적값을 가질 때)에서도 더 멀리 나갈 확률이 큰 단점이 있지만 NAG 방식은 momentum에 의한 이동을 먼저 가정한 뒤 그 자리에서 gradient를 구하므로 적절한 시점에서의 제동에 유용
Adaptive Gradient (Adagrad)
학습률이 너무 작으면 학습 시간이 너무 오래 걸리고, 너무 크면 발산해서 학습이 제대로 이루어지지 않음
Adagrad는 학습 진행 중에 학습률을 줄여나가는 방법
과거의 기울기를 제곱하여 더하는 방식으로 학습을 진행하여 갱신 정도가 약해짐
장점
- 학습률을 크게 설정하여도 점차 작아지므로 빠르게 수렴할 수 있으며 학습이 진행될수록 학습률이 작아지면서 보다 세밀하게 최적화 가능
단점
- 만약 학습을 진행하면서 학습률이 계속해서 작아져서 갱신량이 0이 되면 더이상 학습을 수행할 수 없음
RMSProp
Adagrad의 단점을 보완한 기법
과거의 기울기들을 똑같이 더해가는 것이 아닌 먼 과거의 기울기는 조금만 반영, 최신 기울기는 많이 반영 (지수이동평균)
Adam
Momentum과 Adagrad를 융합
학습률, 일차 모멘텀용 계수, 이차 모멘텀용 계수를 설정할 수 있음
Nadam
Adam에 Momentum 대신 NAG를 적용한 기법