오차 함수는 머신 러닝 모델의 예측값과 실제값 간 차이나는 정도를 통해 현재 모델의 성능을 측정하는 지표로 사용됨
오차 함수는 크게 수치 예측 시와 분류 시로 나눌 수 있음
수치 예측 시 오차 함수
MSE(Mean Sqaure Error)
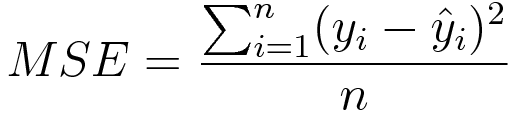
예측값과 실제값의 차이 제곱의 평균
회귀 모델의 주요 손실 함수로 사용됨
차이의 제곱에 인해 실제 값과 거리가 먼 예측(특이값)은 큰 페널티를 받음
RMSE(Root Mean Square Error)
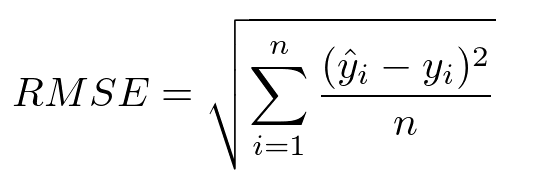
MSE 결과에 루트를 씌운 것
MSE는 오차의 제곱을 사용하기에 실제 오류 평균보다 커지는 특성이 있어 루트를 씌운 RMSE는 값의 왜곡을 줄여줌
MAE(Mean Absolute Error)
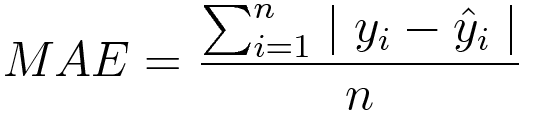
예측값과 실제값 간의 절대 차이 합계의 평균
이상값에 대해 더 강력함
RMSLE(Root Mean Square Logarithmic Error)
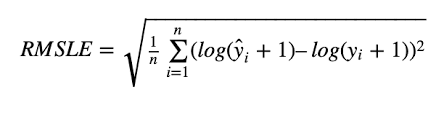
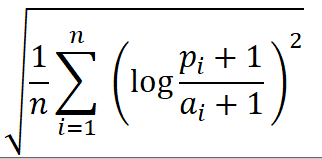
RMSE는 예측값과 실제값의 차 각각을 제곱한 값을 평균내어 루트를 씌운 것
제곱하고 다시 루트를 씌웠으니 그 값의 단위는 예측값과 실제값의 차이 단위와 같음
로그 정규화등을 통한 데이터 분포를 조정하는 전처리 후 해당 산출물에 대한 결과물도 정규화한 값들을 기준으로 모델의 성능을 검증하는데 활용
RMSE에 비해 특이값에 덜 민감
예측값과 실제값의 비율로 상대적 에러를 측정해줌
예측값이 실제값보다 작을 때 더 큰 페널티를 부여
ex) 배달 예정 시간
Binary Cross Entropy
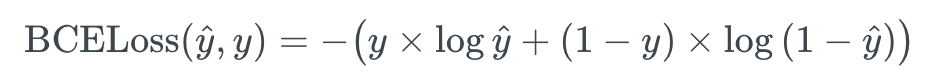
보편적으로 이진 분류 문제에 활용되는 오차 함수
수식에서 y hat은 예측값을 의미하며 y는 실제값을 의미
이진 분류 문제에서 오차 함수는 실제 타겟과 예측 타겟이 다를 때 큰 오차를 주도록 설계됨
일바적으로 모델의 예측값은 sigmoid 활성화 함수의 출력으로 표현되며, sigmoid 출력으로 가질 수 있는 값은 0~1 사이의 값
위 수식에서 실제 값이 0일때는 앞부분의 로그 함수가 사라지고, 실제 값이 1일 때에는 뒤의 log 함수가 사라짐
실제 값은 0과 1 둘 중 하나의 값을 무조건 가지므로 각각의 로그 함수에 대해 생각
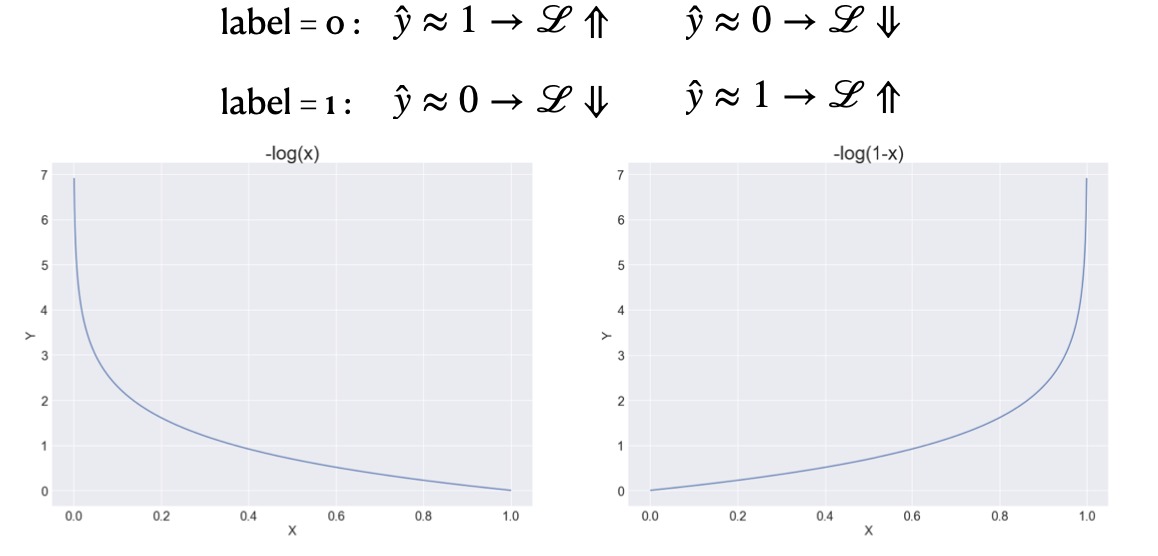
실제 값이 1이 되었을 때는 -log(예측값) 그래프가 되는데, 이 때 예측값이 0에 가까운 경우 그 결과가 가장 크고, 1에 가까운 경우 그 결과가 가장 작은 형태가 됨
실제 값이 0이 되었을 때는 반대로 되며, 결국 예측되는 sigmoid 값이 실제 값과 가까울 경우 오차가 작고, 서로 다를 경우 오차가 큰 형태로 계산되게 하여 오차를 계산
Categorical Cross Entropy
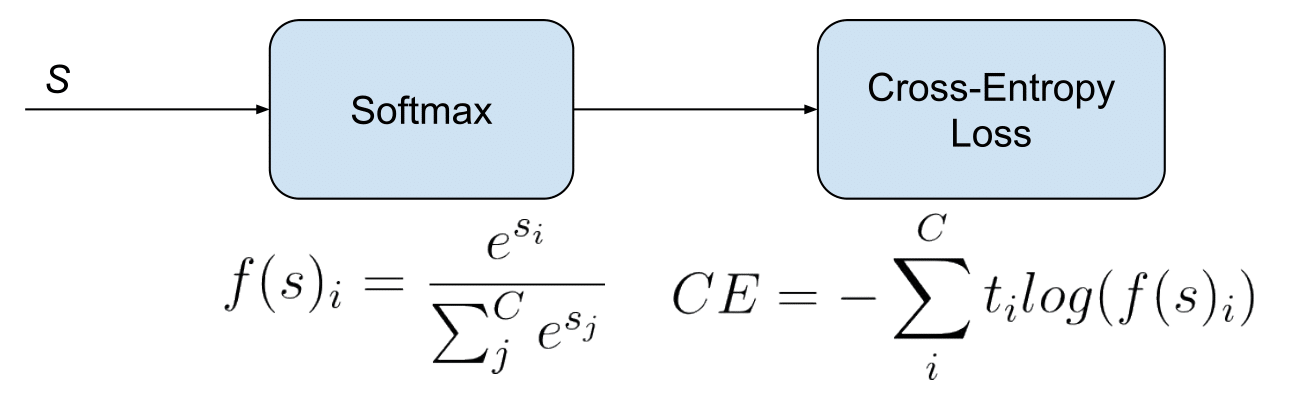
다중 분류에 활용되는 오차 함수
주로 softmax 출력과 함께 사용됨
softmax 출력은 여러 클래스 각각에 대한 확률값
수식의 C는 클래스의 수를 의미
각 클래스에 대하여 실제값과 log(예측값)의 곱을 모두 더한 값의 음수인데, 위의 binary cross entropy 함수의 -log(x)와 유사
실제 타깃 클래스에 해당하는 ti 값은 1일 것이며, 해당하는 경우 log를 취하는 예측 값이 1에 가까울수록 오차는 작고, 작을수록 오차는 커지는 형태
binary cross entropy는 하나의 출력이 실제가 0인 경우, 1인 경우를 구분하여 계산해야 했지만 categorical cross entropy는 실제 예측 타겟에 해당하는 결과가 맞는지만 판단하기에 -log(y)만의 합을 갖고 표현 가능
'Machine Learning > Theory' 카테고리의 다른 글
| 경사 하강법 최적화 알고리즘 - 1 (0) | 2023.09.13 |
|---|---|
| 경사하강법 (Gradient Descent) (0) | 2023.09.13 |
| 딥러닝 모델의 학습 (0) | 2023.09.13 |
| 활성화 함수 종류 (0) | 2023.09.13 |