활성화 함수(Activation Function)
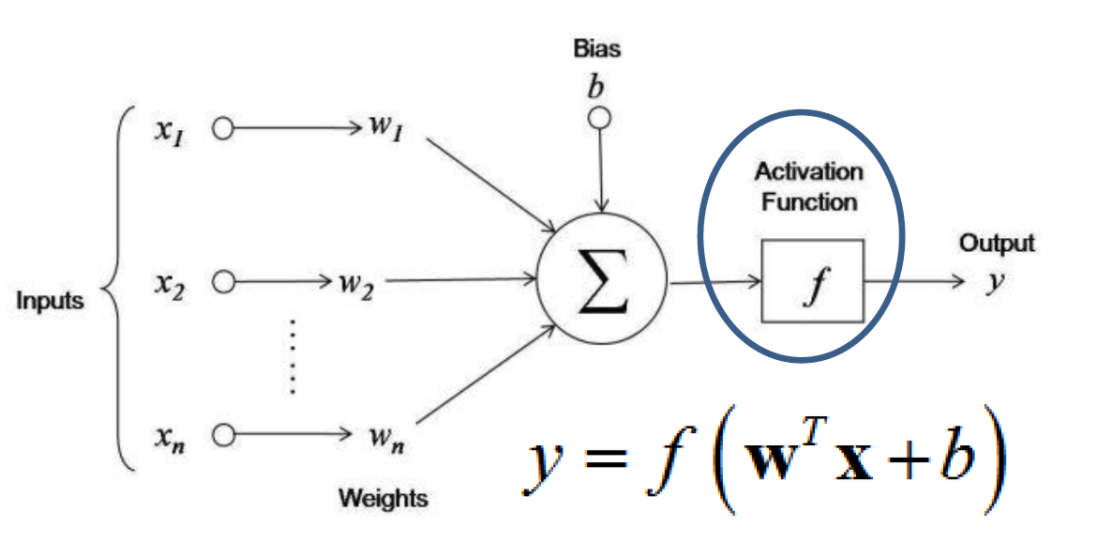
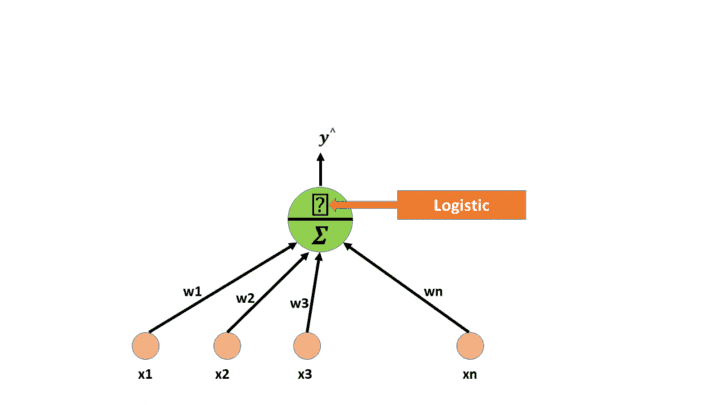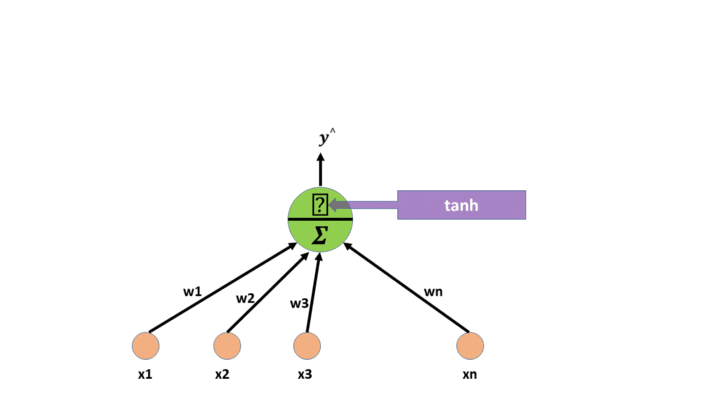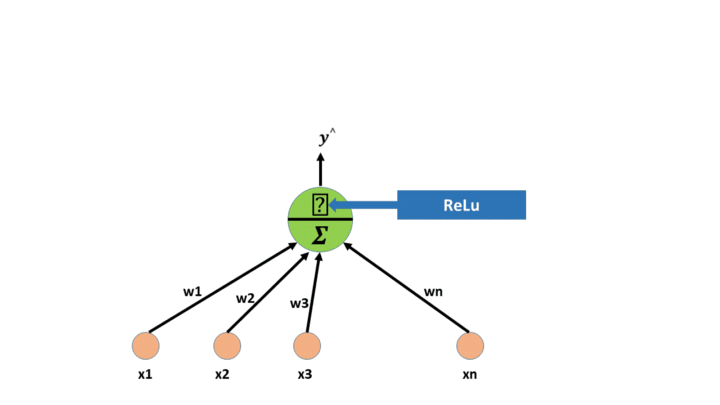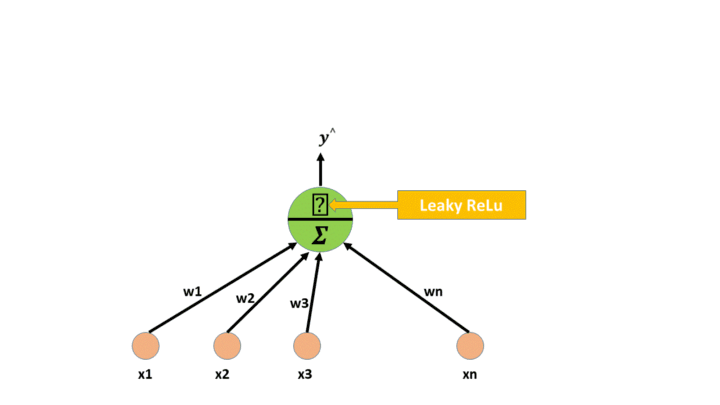
인공신경망에서 노드의 입력은 가중치(w)와 편향(b)을 사용하여 선형 변환이 수행된 이후, 활성화 함수가 적용되어 다음 층으로 전달되거나 예측하는 출력값이 됨
이러한 정보의 흐름을 순방향 전파라고 함
손실 함수(Cost Function, 비용 함수, Loss Function)
모델에서 순방향 전파에 의해 출력된 예측값과 실제값 사이의 오차 계산을 위해 사용되는 함수
모델의 예측 성능을 평가하는 척도
역전파(Backpropagation)
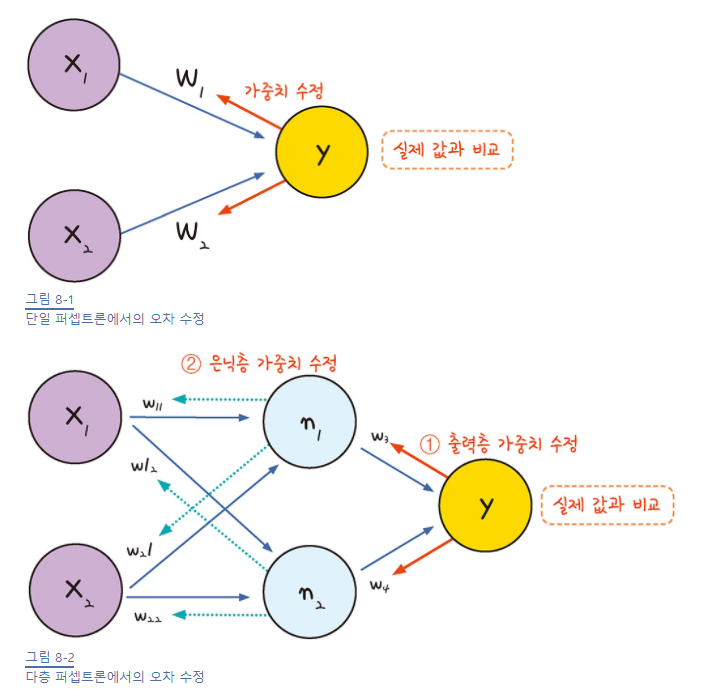
위에서 얘기한 순방향 전파와 반대로 손실정보를 기반으로 모델의 가중치, 편향과 같은 파라미터 벡터를 업데이트하기 위해 모델에 전달하는 과정
경사하강법(Gradient Descent)
역전파는 단순히 가중치와 편향을 업데이트하기 위해 손실의 정보를 전달하는 방식
모델이 더 나은 예측을 수행하기 위해서는 모델의 예측과 실제값 간 차이가 적게 나는 것이 목표
해당 목표를 달성하기 위해 오차가 감소하는 방향, 즉 비용 함수 값이 최소가 되는 방향으로 모델의 파라미터 벡터를 업데이트 하기 위한 방법
※ 경사하강법을 수행하기 위한 일반적인 요구사항으로 미분 가능한 함수, 볼록한 함수라는 목표가 있고, 딥러닝에서 경사하강법은 오차함수를 최소화하기 위해 사용됨
그래서 일반적으로 수치를 예측하는 딥러닝 모델 학습 시 rmse, mae와 같은 손실 함수가 아닌 mse를 학습용 loss로 사용하는 듯 함
활성화 함수 사용 목적
첫 번째 이미지의 y = f(wx + b) 에서의 함수가 활성화 함수
만약 활성화 함수가 없다면 모든 노드의 출력들이 선형적인 형태일 것
ex) f(x) = ax + b, g(x) = cx + d
y = ax + b
z = cy + d
z = c(ax + b) + d → 결국 선형적인 함수
활성화 함수를 적용하지 않는다면 딥러닝에서 층의 의미가 사라짐
대부분의 경우 문제들에 대해 선형 방정식으로 데이터를 잘 모델링 할 수 없음
결국 모델은 입력 데이터와 출력 데이터를 기반으로 데이터를 잘 표현할 수 있는 식을 표현
따라서 활성화 함수는 비선형 함수들을 사용하게 됨
모델의 학습 방법
- 신경망 구조 설계
- 파라미터 벡터 초기화 (가중치, 편향)
- 순전파 (입력이 가중치, 편향, 활성화 함수를 타면서 출력)
- 출력된 예측 값과 실제값의 오차함수 계산
- 역전파를 통해 각 가중치에 대한 편미분 값 계산 및 경사하강법을 통해 오차함수를 최소화하는 방향으로 파라미터 업데이트
- 특정 기준 충족 시 까지 과정 반복
초기의 파라미터 벡터(가중치, 편향)들은 무작위로 초기화되며 데이터를 기반으로 학습이라는 과정을 거쳐 결론적으로 오차가 최소에 가장 근접하게 하는 파라미터 벡터를 찾는 것이 모델 학습의 목표
'Machine Learning > Theory' 카테고리의 다른 글
| 경사 하강법 최적화 알고리즘 - 1 (0) | 2023.09.13 |
|---|---|
| 경사하강법 (Gradient Descent) (0) | 2023.09.13 |
| 오차 함수 종류 (0) | 2023.09.13 |
| 활성화 함수 종류 (0) | 2023.09.13 |